2023. 10. 31. 13:58ㆍ[빅분기]
범주형 자료분석은 자료들이 이산형(discrete)인 경우에 사용한다.
|
|
sucess (성공)
|
fail (실패)
|
|
exposed ( 관심집단 )
|
a
|
b
|
|
unexposed ( 비교집단 )
|
c
|
d
|
1) RR : 비교집단 위험률 대비 관심집단 위험률 ; 상대적 위험도

==> RR은 비교집단 위험률대비 관심집단이 위험률을 나타내기 때문에
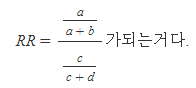
- RR=1 : 무관
- RR>1 : 확률높음
- RR<1 : 확률낮음
2) Odds : 비교집단 승산대비 관심집단 승산
==> Odds는 주어진 환경에서 발생할 확률/그렇지 않을 확률이기 때문에

==> Odds비는 비교집단 승산대비 관심집단이 승산을 나타내기 때문에

3) 카이제곱 (= 교차분석) , 카이제곱 검정은 세가지 분석이 가능하다.
1) 적합도 2) 독립성 3) 동질성
적합도 검정 : 특정분포를 따르는가 | df=k-1
독립성 검정: 두 변수가 독립인가 | df=(r-1)(c-1)
동질성 검정: 각 범주의 모집단이 동질한가 | 계산법은 독립성 검정과 동일
다차원 척도법
다차원척도법은 개체들 사이의 유사/비유사성을 측정해서 개체를 2,3차원 공간에 점으로 표현한다. ( 개체간 근접성과 집단화를 시각적으로 표현 )
장점) 1. 잠재패턴 발견 -> 공간에 기하학적으로 표현
2. 데이터 축소, 데이터 정보발견을 위한 탐색수단
3. 데이터가 만들어진 현상이나 과정에 고유의 의미부여
유클리드 거리 (d) 계산 == 개체간의 유사/비유사성 측정 == 적합/부적합 측정
(s)라는 스트레스값으로 재표현 --> 스트레스 값(S)이 best인 모형 찾자
S=0 ; 완벽, S>0.15; 적합수준이 나쁘다
종류) 1. 계량적 (등간척도/비율척도) 2. 비계량적 (순서척도)
다변량분석은 PCA, 요인분석, 판별분석의 내용을 담고 있다.
1) PCA : 주성분분석은 상관성이 높은 변수들의 선형결합으로 이뤄진
'주성분' 이라는 새로운 변수에 변수들을 요약, 축소하는 기법이다.
장점) 1. 차원축소 -> 데이터 이해 easy
2. 직교하는 축을 찾으므로 rho=0이 되어서 다중공선성 문제해결
3. 차원을 줄였기 때문에 군집분석 수행시 연산속도 개선
주성분 기억률(=주성분변수의 분산) ㅣ 총변동에 대한 설명력을 가진다
누적기억률 > 85% 가 되는 변수까지 선택한다
팔꿈치그림(=Scree plot) : 주성분(x축), 고유치(y축)
2) 요인분석 : 변수간 상관관계 고려해서 비슷한 변수를 묶어서 해로운 잠재요인추출
조건 [ 등간/비율척도, 표본은 100개이상 ]
요인 : 새롭게 생성한 변수집단
요인적재값 : 변수와 요인간 상관계수
--> 이거 제곱하면 해당변수가 요인으로 설명되는 분산비
고유값 : 요인이 설명할 수 있는 변수분산의 총합
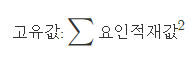
공통성 : 요인이 설명할 수 있는 한 변수의 분산의 양을 백분율로, 즉 요인이 변수의 정보를 얼마나 설명하는가를 나타냄
- 요인 추출방법) 1. 주성분분석 : 주로사용, 총분산 기반 요인추출
2. 공통요인분석: 공통분산만 기반 요인추출
- 주성분분석 ) n개의 입력 변수들이 가지는 총분산을 n개의 주성분으로 다시 나타냄, 먼저 추출된 주성분 요인이 총분산을 많이 설명하도록 순차적으로 추출
--> 총분산 쓰기 때문에 정보손실을 줄이고 총분산을 많이 설명하도록 하는 요인을 효과적으로 추출해서 공통요인분석보다 주로 사용됨.
- 요인수 결정) 1. 고유값 >1 인 요인
2. scree plot의 팔꿈치
- 요인분석 절차)
① 데이터입력
② 상관계수산출
③ 요인추출
④ 요인적재량산출
⑤ 요인회전 ; 요인해석과 패턴을 찾으려보 분산 재분배
⑥ 생성된요인해석
⑦ 요인점수산출
요인회전은 직각(쿼티, 베리, 아퀴멕스)/비직각회전(오블라민) 있음
3) 판별분석 : 집단을 구별할 수 있는 판별함수와 규칙을 만들어 개체가 어느 집단에 속하는지 분류하는 다변량 기법.
조건 [ 독립변수: 등간/비율, 종속변수: 명목/순서 ]
- 판별식) Z(판별점수) = 독립변수들의 선형결합
- 판별식 수) min(집단수-1, 독립변수 수)
- 판별방식) 그룹 내 분산에 비해 그룹간 분산의 차이를 최대화하는 계수탐색
시계열분석은 시간의 흐름에 따른 관측자료분석이다.
- 정상성 : 시계열의 확률적인 성질들이 시간의 흐름에 따라 변하지 않음.
① 평균일정 : 모든시점에 대해 일정, 정상화(=차분:현-전)
② 분산일정 : 시점에 의존X, 정상화(변환)
③ 공분산은 시차에만 의존, 특정시점에 의존X
<=> 시차가 있어야만 공분산 존재가능
=> 항상 평균으로 회귀하려는 경향
=> 평균값 주변 변동폭이 일정
시계열 모형
- 자기회귀 모형(AR) : 자기상관성을 시계열 모형으로 구성
| p시점 전의 자료가 현재 자료에 영향을 주는 특성
| 자기상관함수(ACF) : 시계열 데이터의 자기상관성 파악
| Z=현재시점의 시계열 자료
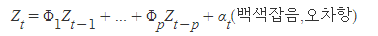
- 이동평균 모형(MA) : 시간이 지날수록 관측치의 평균값이 지속적으로 증가하거나 감소하는 경향을 표현, 언제나 정상성 만족
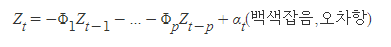
'[빅분기]' 카테고리의 다른 글
| [PART3 요약추가] (0) | 2023.10.31 |
|---|---|
| [빅데이터 모델링] (0) | 2023.10.31 |
| [PART1/PART2 오답노트] (0) | 2023.10.31 |
| [빅데이터 탐색] (0) | 2023.10.31 |
| [빅데이터의 이해] (0) | 2023.10.31 |